Iterative Reconstruction

29 Sep 2018

Reconstruction of CT images is a process to approximate a solution to the problem. Back-projection and Filtered back-projection (FBP) are methods which do fairly well at low computational cost. Technically there is an ideal solution - the best that can be done with the data available; by looking at the problem as an enormous mass of simultaneous equations you reach the ideal solution … at great computational cost.

Iterative reconstruction is that middle ground method. It’s actually not just one method, but a few different variations. It can allow greater image quality to be extracted from the same data when compared to FBP. It deals with certain types of lack of data well in general - as a result it is commonly used in the real world to reduce X-ray dose.

The Method

This is a basic method of an iterative reconstruction algorithm. Starting with our original sinogram, here we simply:

1. Back-project without any filter
2. Create a sinogram of our back-projection reconstruction
3. Take the new sinogram from our original sinogram to get a measure of the error
4. Multiply our error sinogram by a relaxation value (0.5 works well)
5. Back-project our error sinogram (again, no filter)
6. Add our error correction reconstruction to our first back-projection
7. Rinse and repeat

It it worth having some way to determine when to stop. This iterative algorithm will definitely plateau, giving deminishing returns for every iteration.

Some Results

So, here we have our original mathematical phantom:

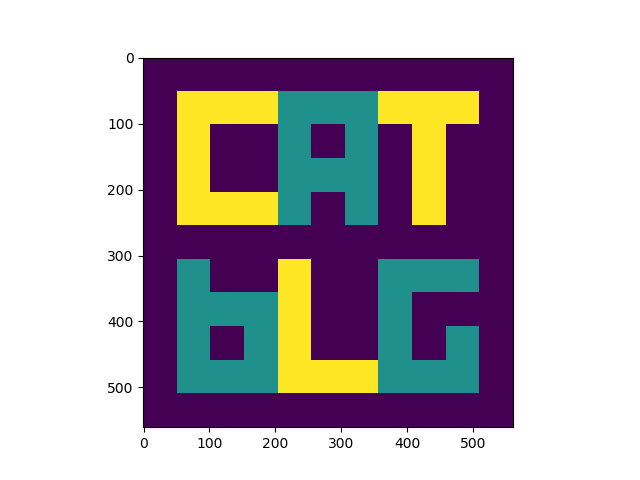
Our 3rd iteration:

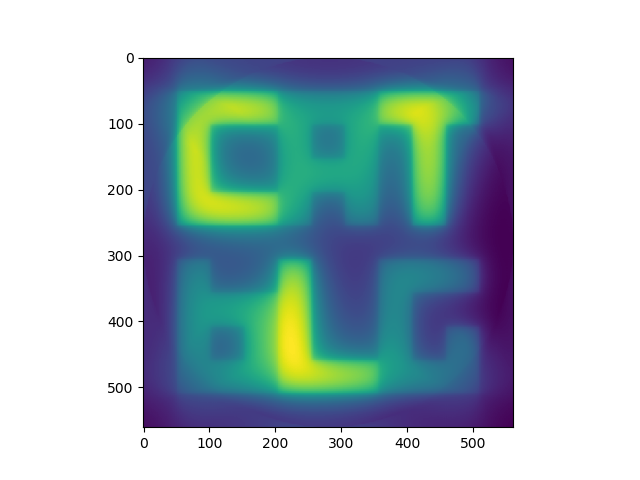
Our 10th iteration:

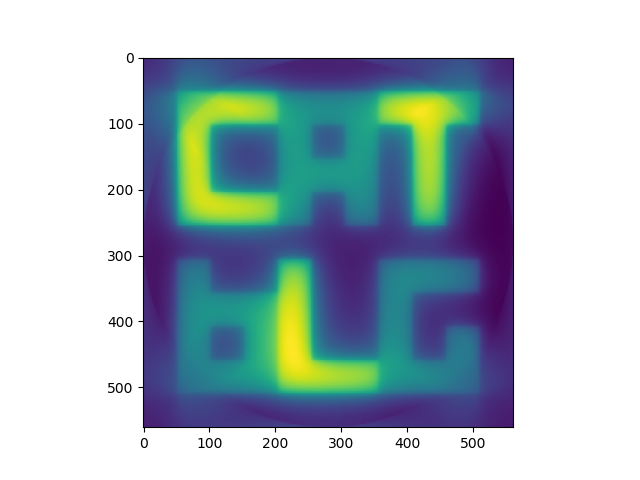
Our 50th iteration:

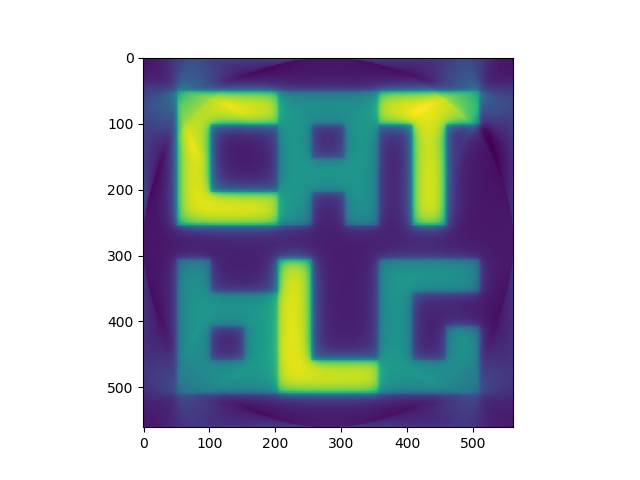
Our 220th iteration:

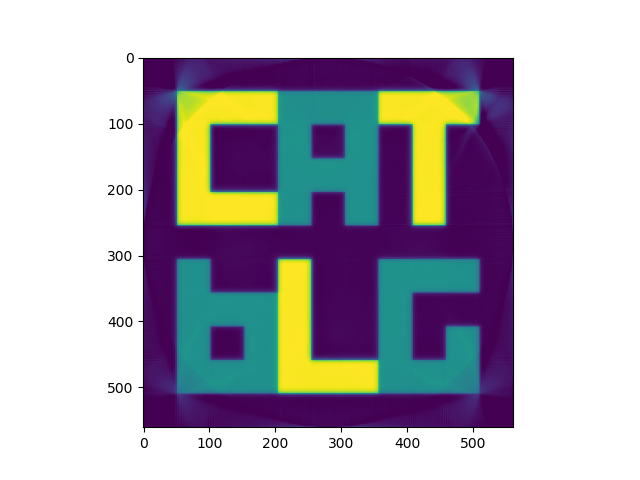
These are all false coloured. They would normally be greyscale, but it is easier to see what is happening in colour.

You can see that the image is progressively getting sharper with each iteration. With the sharpness the actual pixel values are getting closer to the original phantom too - this can’t be seen on the images as the pixel values are re-scaled for the images.